অনুক্রম, অনুক্রমের প্রকারভেদ ও সাধারণ পদ। ৯ম-১০ম উচ্চতর গণিত

$sequence-kinds-of-sequence-and-general-terms-class-9-10-higher-math-mathbd$

অনুক্রম, অনুক্রমের প্রকারভেদ ও সাধারণ পদ

বিষয়বস্তু: অসীম ধারা (৯ম-১০ম উচ্চতর গণিত)

অনুক্রম (Sequence)

কতগুলো রাশি একটি নিয়ম অনুসরন করে ক্রমান্বয়ে সাজানো হলে, সাজানো রাশির সেটকে অনুক্রম বলা হয়। অনুক্রমের প্রত্যেকটি রাশি তার পূর্বের রাশি ও পরের রাশির সাথে একটি সম্পর্ক বজায় রাখে।

উদাহরণ:

2, 4, 6, 8, 10, . . . , , 50

অনুক্রমের রাশিগুলোকে যথাক্রমে $a_1, a_2, a_3, . . . a_n$ দ্বারা প্রকাশ করা হয়। এখানে, $a_1=2, a_2=4, a_3=6, . . ., a_n=50$

সসীম ও অসীম অনুক্রম

যে অনুক্রমের শেষ রাশিটি কত তা বলে দেয়া যায় তাকে সসীম অনুক্রম বলা হয়। যেমন: 2, 4, 6, 8, . . ., 50 অনুক্রমটির শেষ রাশিটি কত জানতে চাওয়া হলে, আমরা নিশ্চয় বলে দিতে পারবো শেষ রাশিটি 50। সুতরাং এই অনুক্রমটি সসীম অনুক্রম। আর যে অনুক্রমের শেষ রাশিটি বলে দেয়া সম্ভব নয় তাকে অসীম অনুক্রম বলা হয়। যেমন: 2, 4, 6, 8, 10, . . . অনুক্রমটির শেষ রাশিটি কত জানতে চাওয়া হলে আমরা তা বলতে পারবো না। এখানে, ‘ . . . ‘ চিহ্নটির অর্থ হলো অনুক্রমটি অসীম পর্যন্ত বিস্তৃত। সুতরাং এই অনুক্রমটি অসীম অনুক্রম।

সমান্তর অনুক্রম

যে অনুক্রমের পাশাপাশি দুইটি রাশির পার্থক্য সর্বদা সমান তাকে সমান্তর অনুক্রম বলে। সমান্তর অনুক্রমের পাশাপাশি দুইটি রাশির পার্থক্যকে সাধারণ অন্তর বলা হয়। এই অনুক্রমের যেকোনো রাশি থেকে তার পূর্বের রাশিটি বিয়োগ করে এই সাধারণ অন্তর নির্ণয় করা হয়।

উদাহরণ:

2, 4, 6, 8, . . . , 28

এখানে,

২য় রাশি – ১ম রাশি = 4 – 2 = 2

৩য় রাশি – ২য় রাশি = 6 – 4 = 2

এভাবে যেকোনো রাশি থেকে তার পূর্বের রাশিটি বিয়োগ করে সর্বদা সমান বিয়োগফল পাওয়া যায় সমান্তর অনুক্রমে। এই বিয়োগফলটি হলো প্রদত্ত অনুক্রমের সাধারণ অন্তর। সাধারণ অন্তরকে সাধারণত d দ্বার প্রকাশ করা হয়।

এখানে, সাধারণ অন্তর, d = 2 ।

সমান্তর অনুক্রমের সাধারণ পদ (n তম পদ)

$U_n = a + (n-1)d$

এখানে, a = ১ম পদ, d = সাধারণ অন্তর, n = পদসংখ্যা।

No.. 1

2, 4, 6, 8, 10, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

১ম পদ a = 2, সাধারণ অন্তর d = 4 – 2 = 2

সমান্তর অনুক্রমের সাধারণ পদ = a + (n-1)d

= 2 + (n-1) \times2

= 2 + 2n – 2

= 2n

$\therefore$ অনুক্রমটির সাধারণ পদ (n তম পদ) = 2n

সাধারণ পদ ব্যবহার করে অনুক্রমের নির্দিষ্ট পদ নির্ণয়

সাধারণ পদ ব্যবহার করে অনুক্রমের যেকোনো পদ নির্ণয় করা যায়।

উদাহরণ:

প্রশ্ন: 2, 4, 6, 8, 10, . . . অনুক্রমটির 50 তম পদটি কত?

উত্তর:

পদ্ধতি-১ (প্রদত্ত অনুক্রমটির সাধারণ পদ ব্যবহার করে)

অনুক্রমটির 50 তম পদ $= 2n = 2 \times 50 = 100$

পদ্ধতি-২ (সমান্তর অনুক্রমের সাধারণ পদ ব্যবহার করে)

অনুক্রমটির 50 তম পদ $= a+(n-1)d = 2+(50-1) \times 2 = 2+98 = 100$

No. 2

1, 3, 5, 7, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

সমান্তর অনুক্রমের সাধারণ পদ = a + (n-1)d

= 1+(n-1)2 [ যেহেতু a=1, d=2 ]

= 1+2n-2

= 2n – 1

$\therefore$ অনুক্রমটির সাধারণ পদ (n তম পদ) = 2n – 1

No. 3

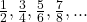$\frac{1}{2}, \frac{3}{4}, \frac{5}{6}, \frac{7}{8}, . . .$ অনুক্রমের সাধারণ পদ নির্ণয়:

অনুক্রমটির সাধারণ পদ = লবের সাধারণ পদ $\div$ হরের সাধারণ পদ

$= \frac{2n-1}{2n}$

$\therefore$ অনুক্রমটির সাধারণ পদ (n তম পদ) $= \frac{2n-1}{2n}$

গুণোত্তর অনুক্রম

যে অনুক্রমের পাশাপাশি দুইটি রাশির অনুপাত সর্বদা সমান থাকে তাকে গুণোত্তর অনুক্রম বলা হয়। গুণোত্তর অনুক্রমের যেকোনো রাশিকে তার পূর্বের রাশি দিয়ে ভাগ করে যে ভাগফল পাওয়া যায় তা হলো অনুক্রমটির সাধারণ অনুপাত। সাধারণ অনুপাতকে সাধারণত r অথবা q দ্বারা প্রকাশ করা হয়।

উদাহরণ:

2, 4, 8, 16, 32, . . . , 1024

এখানে,

২য় রাশি $\div$ ১ম রাশি = $\frac{4}{2} = 2$

৩য় রাশি $\div$ ২য় রাশি = $\frac{8}{4} = 2$

এভাবে গুণোত্তর অনুক্রমের যেকোনো রাশিকে তার পূর্বের রাশি দারা ভাগ করলে ভাগফল সর্বদা সমান পাওয়া যায়।

এখানে, সাধারণ অনুপাত r = 2

গুণোত্তর অনুক্রমের সাধারণ পদ (n তম পদ)

$U_n = ar^{n-1}$

এখানে, a = ১ম পদ, r = সাধারণ অনুপাত, n = পদ সংখ্যা

No. 4

2, 4, 8, 16, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

১ম পদ a = 2, সাধারণ অনুপাত, r = $\frac{4}{2} = 2$

গুণোত্তর অনুক্রমের সাধারণ পদ = $ar^{n-1}$

$= 2 \times 2^{n-1}$ [ যেহেতু a=2, r=2 ]

$= 2^{1+n-1}$

$= 2^n$

$\therefore$ অনুক্রমটির সাধারণ পদ (n তম পদ) $= 2^n$

সাধারণ পদ ব্যবহার করে অনুক্রমের নির্দিষ্ট পদ নির্ণয়

সাধারণ পদ ব্যবহার করে অনুক্রমের যেকোনো পদ নির্ণয় করা যায়।

উদাহরণ:

প্রশ্ন: 2, 4, 8, 16, . . . অনুক্রমটির 10 তম পদটি কত?

উত্তর:

পদ্ধতি-১ (প্রদত্ত অনুক্রমের সাধারণ পদ ব্যবহার কর)

অনুক্রমটির 10 তম পদ $= 2^n = 2^{10} = 1024$

পদ্ধতি-২ (গুণোত্তর অনুক্রমের সাধারণ পদ ব্যবহার করে)

অনুক্রমটির 10 তম পদ $= ar^{n-1} = 2 \times 2^{10-1} = 2 \times 2^9 = 2^{10} =1024$

No. 5

1, 3, 9, 27, 81, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

গুণোত্তর অনুক্রমের সাধারণ পদ = $ar^{n-1}$

$= 1 \times 3^{n-1}$

$= 3^{n-1}$

$\therefore$ অনুক্রমটির সাধারণ পদ (n তম পদ) $= 3^{n-1}$

No. 6

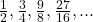$\frac{1}{2}, \frac{3}{4}, \frac{9}{8}, \frac{27}{16}, . . .$ অনুক্রমের সাধারণ পদ নির্ণয়:

অনুক্রমের সাধারণ পদ = লবের সাধারণ পদ $\div$ হরের সাধারণ পদ

$= \frac{3^{n-1}}{2^n}$

$\therefore$ অনুক্রমটির সাধারণ পদ (n তম পদ) $= \frac{3^{n-1}}{2^n}$

মিশ্র অনুপাত

কোনো ভগ্নাংশের অনুক্রমে লব ও হরের রাশিগুলো ভিন্ন ভিন্ন অনুক্রম অনুসরণ করতে পারে। উদাহরণস্বরূপ, কোনো ভগ্নাংশের অনুক্রমে লবগুলো সমান্তর অনুক্রম অনুসরণ করছে আর হরগুলো গুণোত্তর অনুক্রম অনুসরণ করছে এমন থাকতে পারে। আবার এর উল্টোটিও থাকতে পারে অর্থাৎ লবগুলো গুণোত্তর অনুক্রম অনুসরণ করছে আর হরগুলো সমান্তর অনুক্রম অনুসরণ করছে। এই ধরনের ভগ্নাংশের অনুক্রমকে বলা হয় মিশ্র অনুক্রম।

উদাহরণ:

$\frac{1}{2}, \frac{3}{4}, \frac{5}{8}, \frac{7}{16}, . . .$

এখানে, লবগুলো সমান্তর অনুক্রম অনুসরণ করছে আর হরগুলো গুণোত্তর অনুক্রম অনুসরণ করছে।

মিশ্র অনুক্রমের সাধারণ পদ (n তম পদ) নির্ণয়:

No. 7

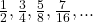$\frac{1}{2}, \frac{3}{4}, \frac{5}{8}, \frac{7}{16}, . . .$ অনুক্রমের সাধারণ পদ নির্ণয়:

সাধারণ পদ = লবের সাধারণ পদ $\div$ হরের সাধারণ পদ

$= \frac{a+(n-1)d}{ar^{n-1}}$

$= \frac{1+(n-1) \times 2}{2 \times 2^{n-1}}$

$= \frac{1+2n-2}{2^{1+n-1}}$

$= \frac{2n-1}{2^n}$

$\therefore$ অনুক্রমটির সাধারণ পদ (n তম পদ) $= \frac{2n-1}{2^n}$

আরো কিছু অনুক্রমের সাধারণ পদ

No. 8

$1, 2, 3, 4, . . .$ অনুক্রমের সাধারণ পদ (n তম পদ) = n

No. 9

$2, 3, 4, 5, . . .$ অনুক্রমের সাধারণ পদ (n তম পদ) = n+1

No. 10

$3, 4, 5, 6, . . . .$ অনুক্রমের সাধারণ পদ (n তম পদ) = n+2

No. 11

$\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, . . .$ অনুক্রমের সাধারণ পদ (n তম পদ) $\frac{n}{n+1}$

No. 12

$1, \sqrt{2}, \sqrt{3}, 2, . . .$ অনুক্রমের সাধারণ পদ (n তম পদ) $= \sqrt{n}$ [ যেহেতু $\sqrt{1}=1, \sqrt{4}=2$ ]

No. 13

$0, \frac{ln2}{2}, \frac{ln3}{3}, \frac{ln4}{4}, . . .$ অনুক্রমের সাধারণ পদ (n তম পদ) $\frac{lnn}{n}$ [ যেহেতু ln1=0 এবং 0 এর নিচে (হরে) মনে মনে 1 আছে ]

অনুক্রমের সাধারণ পদের চিহ্ন

১। অনুক্রমের প্রতিটি রাশি ধনাত্মক হলে সাধারণ পদের চিহ্ন হবে ধনাত্মক।

উদাহরণ

$\frac{1}{3}, \frac{2}{4}, \frac{3}{5}, \frac{4}{6}, . . .$

অনুক্রমটির সাধারণ পদ $= \frac{n}{n+2}$

২। অনুক্রমের প্রতিটি রাশি ঋণাত্মক হলে সাধারণ পদের চিহ্ন হবে ঋণাত্মক।

উদাহরণ

$- \frac{1}{2}, - \frac{2}{3}, - \frac{3}{4}, - \frac{4}{5}, . . .$

অনুক্রমটির সাধারণ পদ $= - \frac{n}{n+1}$

৩। অনুক্রমের বিজোড় পদগুলো ঋণাত্মক হলে সাধারণ পদে গুণের আকারে $(-1)^n$ থাকবে।

উদাহরণ

$- \frac{2}{3}, \frac{3}{4}, - \frac{4}{5}, \frac{5}{6}, . . .$

অনুক্রমটির সাধারণ পদ $= (-1)^n . \frac{n+1}{n+2}$

৪। অনুক্রমের বিজোড় পদগুলো ধনাত্মক হলে সাধারণ পদে গুণের আকারে $(-1)^{n+1}$ থাকবে।

উদাহরণ

$\frac{2}{3}, - \frac{3}{4}, \frac{4}{5}, - \frac{5}{6}, . . .$

অনুক্রমটির সাধারণ পদ $= (-1)^{n+1} . \frac{n+1}{n+2}$

বিশেষ ধরণের অনুক্রমের সাধারণ পদ

No. 14

0, 1, 0, 1, 0, 1, . . .

অনুক্রমটির সাধারণ পদ (n তম পদ) $= 0.5 + (-1)^n \times 0.5$ [সংকেত: 0.5-0.5=0, 0.5+0.5=1]

No. 15

1, 0, 1, 0, 1, 0, . . .

অনুক্রমটির সাধারণ পদ (n তম পদ) $= 0.5 + (-1)^{n+1} \times 0.5$

No. 16

0, 2, 0, 2, 0, 2, . . .

অনুক্রমটির সাধারণ পদ (n তম পদ) $= 1 + (-1)^n$ [সংকেত: 1-1=0, 1+1=2]

No. 17

2, 0, 2, 0, 2, 0, . . .

অনুক্রমটির সাধারণ পদ (n তম পদ) $= 1 + (-1)^{n+1}$

No. 18

0, 3, 0, 3, 0, 3, . . .

অনুক্রমটির সাধারণ পদ (n তম পদ) $= 1.5 + (-1)^n \times 1.5$ [সংকেত: 1.5-1.5=0, 1.5+1.5=3]

No. 19

3, 0, 3, 0, 3, 0, . . .

অনুক্রমটির সাধারণ পদ (n তম পদ) $= 1.5 + (-1)^{n+1} \times 1.5$

No. 20

2, 3, 2, 3, 2, 3, . . .

অনুক্রমটির সাধারণ পদ (n তম পদ)

$= 2, 0, 2, 0, 2, 0, . . .$ অনুক্রমের সাধারণ পদ $+$ $0, 3, 0, 3, 0, 3, . . .$ অনুক্রমের সাধারণ পদ

$= \{1 + (-1)^{n+1}\} + \{1.5 + (-1)^n\times 1.5\}$

যাচাই:

2, 3, 2, 3, 2, 3, . . .

১ম পদ = $= \{1 + (-1)^{1+1}\} + \{1.5 + (-1)^1 \times 1.5\} = (1+1)+(1.5-1.5)=2+0=2$

২য় পদ = $= \{1 + (-1)^{2+1}\} + \{1.5 + (-1)^2 \times 1.5\} = (1-1)+(1.5+1.5)=0+3=3$

$\therefore$ অনুক্রমটির সাধারণ পদ (বা n তম পদ) সঠিকভাবে কাজ করছে।

নিজে করি

নিচের অনুক্রমগুলোর সাধারণ পদ নির্ণয় করি:

১। $\frac{1}{2}, - \frac{2}{3}, \frac{3}{4}, - \frac{4}{5}, . . .$

২। $\frac{1}{2}, 1, \frac{3}{2}, 2, \frac{5}{2}, . . .$

৩। $5, \frac{5}{3}, \frac{5}{9}, \frac{5}{27}, \frac{5}{81}, . . .$

৪। $5, 4, 5, 4, 5, 4 , . . .$

May 26, 2023

অনুক্রম, অনুক্রমের প্রকারভেদ ও সাধারণ পদ। ৯ম-১০ম উচ্চতর গণিত

অনুক্রম, অনুক্রমের প্রকারভেদ ও সাধারণ পদ

বিষয়বস্তু: অসীম ধারা (৯ম-১০ম উচ্চতর গণিত)

অনুক্রম (Sequence)

সসীম ও অসীম অনুক্রম

সমান্তর অনুক্রম

সমান্তর অনুক্রমের সাধারণ পদ (n তম পদ)

2, 4, 6, 8, 10, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

সাধারণ পদ ব্যবহার করে অনুক্রমের নির্দিষ্ট পদ নির্ণয়

1, 3, 5, 7, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

$\frac{1}{2}, \frac{3}{4}, \frac{5}{6}, \frac{7}{8}, . . .$ অনুক্রমের সাধারণ পদ নির্ণয়:

গুণোত্তর অনুক্রম

গুণোত্তর অনুক্রমের সাধারণ পদ (n তম পদ)

2, 4, 8, 16, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

সাধারণ পদ ব্যবহার করে অনুক্রমের নির্দিষ্ট পদ নির্ণয়

1, 3, 9, 27, 81, . . . অনুক্রমের সাধারণ পদ নির্ণয়:

$\frac{1}{2}, \frac{3}{4}, \frac{9}{8}, \frac{27}{16}, . . .$ অনুক্রমের সাধারণ পদ নির্ণয়:

মিশ্র অনুপাত

মিশ্র অনুক্রমের সাধারণ পদ (n তম পদ) নির্ণয়:

$\frac{1}{2}, \frac{3}{4}, \frac{5}{8}, \frac{7}{16}, . . .$ অনুক্রমের সাধারণ পদ নির্ণয়:

আরো কিছু অনুক্রমের সাধারণ পদ

অনুক্রমের সাধারণ পদের চিহ্ন

বিশেষ ধরণের অনুক্রমের সাধারণ পদ

নিজে করি

0 responses on "অনুক্রম, অনুক্রমের প্রকারভেদ ও সাধারণ পদ। ৯ম-১০ম উচ্চতর গণিত"

Leave a Message Cancel reply